整数 の 問題
入試問題での「整数の問題」というと皆さんは どんな問題を思い出されるでしょうか? 私自身は,「数学の現代化」が叫ばれていたころ, 中学入試用の問題集で,ガウス記号と合同式を初 めて知り,おもしろいと思ったことを覚えていま す。.

整数 の 問題. 2 整数問題の攻略(原則編) まずはじめに,整数問題攻略の4 つの原則(+α) を述 べる.これらは,ほとんど当たり前のことだが,意外と 頭に入っていない(意識していない) 人もいると思うの で確認しておこう.この4 つの原則(+α) は常識として これから使っていくので,しっかりと頭に入れておいて. 岡山大 ガウス記号 年9月4日 9月 3, ;. 問題1 ★★★ ☆☆ 正の整数nとk(0≦k≦n)に対して は正の整数である事実を使ってよいものとする。.
整数問題はどうして難しいの? ではどうして整数問題は難しいと感じてしまうのでしょうか? その理由の1つとして、 答えにたどり着くまでの道筋が一見遠く見えるから です。 問題をただ眺めるだけでは用いるべき解法が分からないので、自身のストックした解法からひとつひとつ試していか. 整数問題は、その名の通り整数を扱った問題です。簡単な例をあげると… こんな問題です。易しいように見えても、実際に解こうとすると意外と解けない!上の問題の場合、答えは 6組 あります。全部数え切れたかな?. 右の例では,整数係数の多項式を整数係数の多項式で割ったときに,商も余りも有理数(分数)の係数になっている. (2) 整数係数の多項式を整数係数の多項式で割ったときの商と余りは,整数になるとは限らない.一般には有理数.
最大公約数g について, 次の各条件 の下でa;. 整数問題 99題 演習1 次の式を満たす正の整数x;y の値を求めよ。 x3y xy3 x2y +xy2 x3 +y3 = 15 1977 芝浦工業大学 x3y xy3 x2y +xy2 x3 +y3 = 15, xy(x y)(x+y) xy(x y) (x y) x2 +xy +y2 = 15, (x y) x2y +xy2 x2 2xy y2 = 15, (x y)(x+y)(xy x y) = 3 5 x;y は正の整数だから、 x+y = 3;5;15 ( i ) x+y = 3 のとき、 (x y)(xy 3) = 5, (x y;xy 3) = (1;5);(5;1. 整数問題は次の13種のパターンに分類できるのです。 1不定方程式や不等式の問題 本来は解けない問題を、整数という条件を適用して因数分解・素因数分解などを利用して解く問題です。もっとも代表的な整数問題といえます。 例題.
整数問題 年8月23日 8月 22, ;. 問題 整数a、bについて x^4+ax^2+b=0の4つの解を考えるとき、 誤差が絶対値0.05であるような近似解として-3.45、-0.61、0.54、3.42がわかっている場合、 真の解を小数点第二位まで求めよ。 (東京大学・19年). 整数問題 年8月日 8月 19, 整数問題 素数 年8月18日 8月 17, ;.
指針)整数問題というより個数処理・数列の和の問題。d −a = k(k = 1,2, ···, n −1)であるも のの個数pk がk で表せる。 04 年度(後期–理) n を自然数とする。xy 平面内の、原点を中心とする半径n の円の、内部と周をあわせたもの をCn であらわす。. 小学2年~6年生向け 算数の練習問題プリントです。中学受験生向けの算数プリント集もあり。栄光ゼミナールの約7万名の生徒が自宅や教室で毎日挑戦している問題データベースから、定番の問題を集めて大公開しています。 栄光ゼミナール内での難易度が載っている問題もありますので、ぜひ. .
7) 任意の正整数n に対して, 32n 1 + 5n は4 の倍数であることを示せ. == 整数の入試問題2 ==. 上智大 整数解を持つ2次方程式 年8月12日 8月 11,.
10) 0 < a ≦ b なる整数a;. 2 AIME 1986の問題 問題4 n3 +100 がn +10 で割り切れるような正の整数n の最大値を求めよ. (AIME 1986 の問題5) 原題はAmerican Invitational Mathematics Examination の 「Find the largest integer n such that n +10 divides n3 +100. Mが2以上の整数のとき、 がmで割り切れるための必要十分条件を求めよ。 (06年 早稲田大学:政経).
9) 任意の整数n に対して, n5 n は30 の倍数であることを示せ. 任意の非負整数は,四つの非負整数の平方の和として表せる。 例えば,$2=1^2+1^2+0^2+0^2$,$15=3^2+2^2+1^2+1^2$ などです。 ラグランジュの定理の証明は英語のサイトを探せばいろいろなものが見つかります。. この記事では整数問題に関する悩みや疑問を解決していきます!センター試験の選択問題や難関大学の2次試験で出題される 整数問題 ですが、「しっかりと対策したことがない」という人が多いのではないでしょうか。 この記事を読んで整数問題の対策をし、得意分野にしていきましょう!.
整数問題も高校生が苦手とする分野のひとつ。 しかし小学校の時、あるいは小学校に入学する前から整数は 我々の生活に馴染み深い ので取り組みやすいが、いざ問題を解こうと思うと、その方法を知らなけてば解けない。. 整数問題① 年8月15日 8月 14, ;. 今日は『イブ』ですね。 ・・・。 今日は『イブ』なんですけど 僕は国家試験の勉強です。 今日は『イブ』ですね・・・。 ~~~~~ 東大医学部発.
Amazonで大山壇の数学 整数 分野別標準問題精講。アマゾンならポイント還元本が多数。大山壇作品ほか、お急ぎ便対象商品は当日お届けも可能。また数学 整数 分野別標準問題精講もアマゾン配送商品なら通常配送無料。. 整式の除法を用いて解くことができる. 解x3 +100 をx +10 で割り算をすると x2 − 10x +100.

14年10月 怜悧玲瓏 高校数学を天空から俯瞰する

伝説の京大入試数学 整数問題 論証ミスで大幅減点 Youtube

2006年 東大数学 文系第3問 整数 3文字の3乗の和 存在証明 東大に文理両方で合格した男が綴る 受験の戦略
整数 の 問題 のギャラリー

年整数問題 A 2 B 2 C 2 Youtube

整数問題へのアプローチ 18 不定方程式を合同式で解く 怜悧玲瓏 高校数学を天空から俯瞰する

整数問題 各桁の和

整数問題にチャレンジ

整数問題の解き方は 大学入試の難問 良問を例に解説 東大医学部生の相談室

整数問題は13パターン 京極一樹の数学塾

整数問題 まなべーと

小学生の算数 分数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生

整数問題 工夫して解きたい式の値の問題 暇つぶしに動画で脳トレ

メルカリ 2 週間で完成 整数問題 入試対策編 参考書 450 中古や未使用のフリマ

小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生

超良問 整数問題の解き方は センスや閃きに頼らない3つの鉄則パターンを解説 Youtube

灘中解説速報 18年第6問 整数問題 算数星人のweb問題集 中学受験算数の問題に挑戦

高校数学a 整数 不定方程式の最重要発想 不等式による絞り込み 受験の月

整数問題へのアプローチ 37 オイラーの定理の利用例 怜悧玲瓏 高校数学を天空から俯瞰する

整数問題

整数問題へのアプローチ 16 剰余類の性質を利用する問題例 怜悧玲瓏 高校数学を天空から俯瞰する

京都大学 18 年文理共通 整数問題 駿台予備学校の解答について 丸亀数理塾

高校数学a 約数と倍数 整数問題の極意 受験の月

マスター オブ 整数 大学への数学 哲也 栗田 邦彦 福田 本 通販 Amazon

今年度の大学受験では 新課程による整数問題の変化に要注意 ベネッセ教育情報サイト

整数問題へのアプローチ 49 裏互除法完成版の証明 1 怜悧玲瓏 高校数学を天空から俯瞰する

Paypayフリマ 大数ゼミ 整数問題完全攻略ゼミ 板書 解説4 スポット講習

整数問題は13パターン 京極一樹の数学塾

数学検定 対策講座 準2級 3級 整数問題 Youtube

整数にまつわる問題を京大数学の入試問題を使って慣れる 京大数学良問から整数を学ぶ 物理u数学の友 質問 悩みに回答します

高校数学a 整数 指数型の不定方程式と整数分野の重要手法 受験の月

割り切れる小数 整数 問題 069 400

2019夏 河合東大オープン 文系数学第4問の解説 整数 互いに素 分数式が整数になる条件 東大に文理両方で合格した男 平井基之による受験戦略の公式

自然数 整数の問題 中学数学 寺子屋塾の復習サイト

2週間で完成 整数問題 安田 亨 本 通販 Amazon

1997年 東大数学 文系文系第1問 強化帰納法 3項間漸化式 対称式 東大に文理両方で合格した男が綴る 受験の戦略

整数問題へのアプローチ 14 合同式でよくある誤用 解答例 怜悧玲瓏 高校数学を天空から俯瞰する

整数問題はどうすれば出来るようになりますか 受験で実力を得点に変えよう 家庭教師の心がけ

整数問題 5to Math Twitter

整数問題の解き方は 大学入試の難問 良問を例に解説 東大医学部生の相談室

12 二項定理 多項定理 京極一樹の数学塾

整数問題bot Seisu Bot Twitter

整数と三次方程式に関する問題 2018年度前期日程の九州大学理系入試問題から 身勝手な主張

大学入試数学の問題

数学a 第3章 整数 問題1 株 たのしい数学模範解答作成社

整数問題は13パターン 京極一樹の数学塾

整数問題ぽい問題 中学数学に関する質問 勉強質問サイト

灘中解説速報 17年第6問 整数問題abc 算数星人のweb問題集 中学受験算数の問題に挑戦
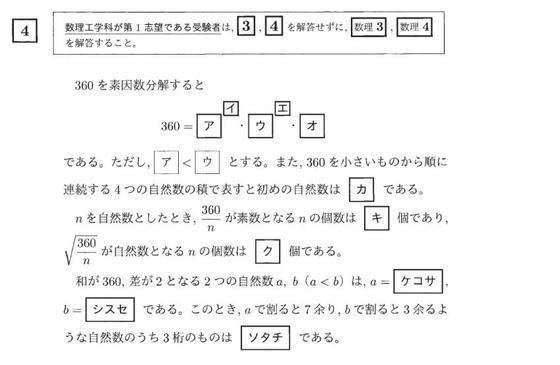
既約分数に関する整数問題です 大学入試数学問題の解説 解答

必要条件で絞り込む 整数問題 Satoooh Blog

2次関数 が整数となるnの値は 数学の偏差値を上げて合格を目指す

整数問題は13パターン 京極一樹の数学塾

話題の今年の京大の理系数学の整数問題の発想の源泉の正体 京大16理系数学2 受験で実力を得点に変えよう 家庭教師の心がけ

整数問題bot 今月の東進数学コンクール面白いしおすすめ是非解いて 整数問題とは言ってない

整数の問題 高校受験編 ネコネコ算数数学ページ

一橋大 数学の問題 整数 数学 さくら教育研究所 Skredu

整数問題へのアプローチ 19年東京大学理系数学第4問 受験で実力を得点に変えよう 家庭教師の心がけ

センター数学の裏技 穴に入るのは全て整数であることを強烈に意識せよ 受験の月

整数問題 中学生が解け 東大生が間違えた超良問 ひっかけ注意 Youtube

整数問題 算数星人のweb問題集 中学受験算数の問題に挑戦

整数問題 高校数学に関する質問 勉強質問サイト

素数を扱う整数問題の研究 過程 紫陽花の咲く物語

大学入試問題 2016年度 2 北海道大学文系前期日程の整数問題 身勝手な主張

整数の問題 理数研究塾 南流山校

中3数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所

合同式を用いた整数問題です 自らの回答において間違えた箇所 高校数学に関する質問 勉強質問サイト

大学入試数学の問題

整数問題 高校数学に関する質問 勉強質問サイト

小学6年生の算数 分数 整数のかけ算 練習問題プリント ちびむすドリル 小学生

数学 For 大学受験 問題 整数問題 Mathworld4 整数の性質
整数問題の解き方は 大学入試の難問 良問を例に解説 東大医学部生の相談室

数学 整数 分野別標準問題精講 大山壇 本 通販 Amazon

阪大理系数学ー整数問題難しい ー 虚空が数学をやるブログ

整数問題 高校数学に関する質問 勉強質問サイト

小学6年生の算数 分数 整数のわり算 練習問題プリント ちびむすドリル 小学生

高校 数学 整式が の倍数であることを証明する問題 整数 数学a 質問解答編 質問ありがとうございます 行間 ぎょうのあいだ 先生

千葉大 数学の問題 整数 数学 さくら教育研究所 Skredu

素数を含んだ整数の方程式の問題の解説ほか 高校数学の達人 河見賢司のメルマガ 2018年11月13日 高校数学の勉強法 河見賢司のサイト

整数問題の解法1 東大に文理両方で合格した男 平井基之による受験戦略の公式

東京都 b17 整数問題 岡野朋一 Note

9 多項式の整数性 割り算などの問題 京極一樹の数学塾

メルカリ 佐々木隆宏の整数問題が面白いほどとける本 参考書 750 中古や未使用のフリマ

整数問題の解き方は 大学入試の難問 良問を例に解説 東大医学部生の相談室

大学入試問題 25 16東工大4 整数 得点を増やす方法を教えます 困ってる人の手助けします 1p500円より

灘中2019年 整数問題ー 中学受験算数の良問 難問 基本問題

整数問題の解き方は 大学入試の難問 良問を例に解説 東大医学部生の相談室

数学問題006 京大の整数 Satoooh Blog

数学 整数問題 高校数学に関する質問 勉強質問サイト

北海道大学の整数問題の解説ほか 高校数学の達人 河見賢司のメルマガ 2018年8月28日 高校数学の勉強法 河見賢司のサイト

整数問題の考え方の解説など 高校数学の達人 河見賢司のメルマガ 11月20日 高校数学の勉強法 河見賢司のサイト

整数問題

数学 整数問題 高校数学に関する質問 勉強質問サイト
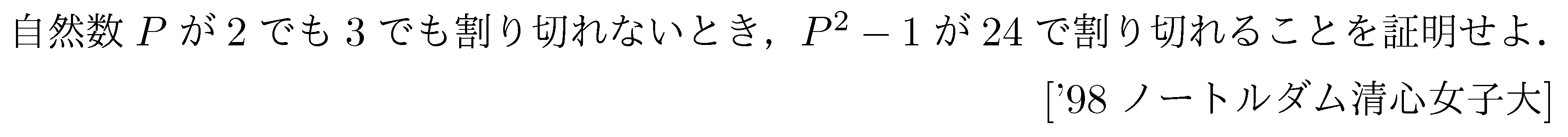
大学入試数学の問題

整数問題の難問 良問3選 解き方のコツやおすすめ参考書を解説します 遊ぶ数学

数論問題 数学の星

2016年 東大文系数学 第4問 小学生でも解ける 整数 合同式 東大に文理両方で合格した男が綴る 受験の戦略

秋田大学の整数問題についての質問です Clear

整数問題 各桁の和

九大数学ー学習効果の高い整数問題ー 虚空が数学をやるブログ

整数とは 小学生でも簡単にわかる問題で 違いを覚えよう 中学や高校の数学の計算問題

整数問題 数学って面白い



